PERSAMAAN EKSPONEN DAN SIFAT SIFATNYA

 

Pengertian Persamaan Eksponen

Persamaan eksponen yaitu sebuah persamaan yang eksponennya juga mengandung peubah x dan tidak menutup kemungkinan bilangan pokoknya juga mengandung peubah x. Sifat Operasi Bilangan Berpangkat Bulat a m x a n = a m + n.

Sifat – Sifat Persamaan Eksponen Berdasarkan Pangkatnya

Sifat – sifat persamaan eksponen sederhana banyak sifatnya, berikut ini sifat – sifat persamaan eksponen berdasarkan pangkatnya adalah :

1. Pangkat Bulat Positif (m dan n bulat positif )

• am. an = am+n
• am/an = am-n
• (am)n = am.n
• (ab)m = am. bm
• (a/b)m = am/bm

2. Pangkat Nol 

• a0 = 1, dengan syarat a ≠ 0

3. Pangkat Bulat Negatif ( n positif )

• a-n = 1/an , atau 1/a-n = an

4. Pangkat Bilangan Pecahan

• a1/n = n√a
• am/n = n√am = ( n√a)m

  Sifat Bilangan Eksponen

  Pertama :

  amxan = nm+n (apa bila di kali maka pangkat nya akan di tambah)

  Contoh : 62x63=62+3=65

  Kedua :

  am :an =am–n  (apa bila di bagi maka sebalik nya pangkat nya harus di kurang)

  Contoh : 85:83=85 – 3=82

  Ketiga :

  (am)n=amxn  (apa bila di dalam kurung  maka pangka tnya harus di kalikan)

  Contoh : (92)3 =92 x 3=96

  Keempat :

  (axb)m=amxbm

  Contoh : (4×5)2=42.52

  Kelima :

  Sifat yang ke lima , memiliki syarat “b”atau penyebut b tidak boleh sama dengan nol (0).

  (a/b)m = am/bm

  Contoh :

  (5/3)2 = 52/32

  Ke enam :

  Pada sifat yang ke enam, apabila (an) di bawah nya bilangan positif, jadi saat di pindahkan ke atas berubah menjadi bilangan negatif. Begitu juga sebalik nya, apabila(an) di bawah nya adalah bilangan negatif, maka saat di pindahkan ke atas otomatis berubah menjadi bilangan positif.

  Perhatikan rumus di bawah ini :

  

  Bilangan Eksponen

  Ke tujuh :

  Pada sifat yang ke tujuh, kita bisa lihat bahwa terdapat akar pada n dari am. Ketika di sederhanakan, maka akar pada n akan menjadi penyebut dalam blangan dan akar m menjadi penyebut pembilang.

  Bersamaan syarat n wajib lebih besar atau = 2.

  Contohnya rumus di bawah ini :

  

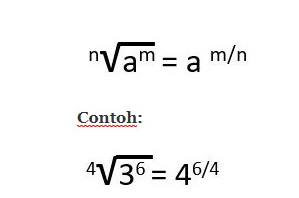
  Bilangan Eksponen

  Ke – 8 :

  Bilangan eksponen nol sama persis dengan a=1.

  Contohnya :

  4=1

  8=1

  11=1

  Memiliki syarat a tidak boleh sama dengan nol.

  Bentuk Bilangan Eksponen

  Bilangan Eksponen Negatif

  Apabila M dan N ialah bilangan bulat positif jadi :
  a-n=1/an
  Contoh :
  3-4=1/34=1/81

  Bilangan Eksponen Pecahan

  Rumus : a1/n = n√a

  Contoh :
  21/2=√2
  21/3=3√2

  Bilangan Eksponen Nol (0)

  Apabila a≠0 jadi a=1 atau a tidak boleh sama dengan hasil 0.